Vector Autoregression

Resources

• Kevin Kotze’s notes on VAR
• Kevin Kotze’s notes on SVAR

Introduction

In this post, I will look at some examples of VAR models, their impulse response functions, and the traditional variance decomposition.

The structural and reduced form VAR models

Consider the simplest two-variable first-order (one lag) VAR system,

Both \(x_t\) and \(z_t\) are assumed to be stationary, and \(\epsilon_{xt}\) and \(\epsilon_{zt}\) are uncorrelated white noise processes with standard deviation \(\sigma_x\) and \(\sigma_z\). In this system, \(x_t\) and \(z_t\) affect each other contemporaneously. The coefficients \(b_{12}\) and \(b_{21}\) decide the magnitude to which a shock in \(x_t\) contemporaneously affect \(z_t\) and vice versa. Note that, a shock in \(\epsilon_{xt}\) affects \(z_t\), however it does not affect \(\epsilon_{zt}\).

However, equations (1) and (2) cannot directly be estimated using OLS because of the simultaneous equation bias since the regressors and the error terms would be correlated due to the contemporaneous effects. Therefore, the common idea is to transform this system. Consider Equations (1) and (2) in its matrix notation,

which is equivalent to,

Equation (4) is called the structural form of the VAR.

We can obtain the reduced form VAR by pre-multiplication by \(B^{-1}\),

where \(A_0 = B^{-1} \Gamma_0\), \(A_1=B^{-1} \Gamma_1\), and \(e_t = B^{-1}\epsilon_t\).

This means that we can write the system of the reduced form as,

where \(a_{i0}\) is defined as element \(i\) of the vector \(A_0\), \(a_{ij}\) as the element in row \(i\) and column \(j\) of the matrix \(A_1\), and \(e_{it}\) as element \(i\) of the vector \(e_t\).

The reduced form directly expresses each endogenous variable as a function of lagged values of all the endogenous variables in the system plus a shock. The reduced form is obtained when the system of equations is invertible and the endogenous variables are not explicitly dependent on contemporaneous values of other endogenous variables in the system.

The structural form differs from the reduced form in that it includes contemporaneous terms on the right-hand side of the equations. These contemporaneous terms represent the theoretical relationship between the variables, which might be suggested by economic theory. To analyze the structural VAR (SVAR), you need to apply identification restrictions to \(B\) and possibly other parameters to uniquely determine the model. This is because the contemporaneous coefficients in are not identifiable purely from the data without additional theoretical or empirical assumptions.

We can note that when \(B=I\) the reduced form system and the structural form coincide. However, depending on how the model are estimated, e.g., if you use pre-built packages the full VAR analysis can differ between the two methods. Specifically, when calculating the impulse responses (which I discuss later in the post) the reduced form typically uses the Cholesky decomposition to orthogonalize the shocks. When using Cholesky decomposition on the reduced form VAR, you’re introducing an artificial ordering of variables, which implicitly imposes a certain structure of contemporaneous effects. This structure dictates that shocks to the first variable in the ordering can affect all other variables contemporaneously, but not vice versa, and so on for each variable according to its position in the order. However, if you estimate an SVAR with \(B=I\), you impose no contemporaneous effects in the IRFs. If you want to use the reduced form without contemporaneous effects you need to set the off-diagonal elements of the variance-covariance matrix equal to zero. The off-diagonal elements can be different from zero if there are contemporaneous effects in the data.

In order to investigate how the contemporaneous relationships affect the reduced form VAR, lets again consider the Equations (6) and (7). It is important to note that the error terms are correlated in this situation. Since,

where

and

Therefore, the elements of \(e_t\) are,

Since both \(\epsilon_{xt}\) and \(\epsilon_{zt}\) are white noise processes, it means that both \(e_{1t}\) and \(e_{2t}\) have zero means and constant variances and are individually serially uncorrelated. The zero means can easily be verified by taking the expected value,

The variances are equal to,

The variances are also time independent with no autocorrelation, e.g., \(\mathbb{E} e_{1t} e_{1t-i} = 0\). However, \(e_{1t}\) and \(e_{2t}\) are correlated, and their covariance is,

In the general case, Equation (17) will not be zero. It will only be zero when there is no contemporaneous effects between \(x_t\) and \(z_t\), as then \(b_{12}=b_{21}=0\). In the general case, it is helpful to define the variance-covariance matrix of the shocks \(e_{1t}\) and \(e_{2t}\) as,

We write the variances and the covariance without a time subscript because they are time independent.

Transforming an SVAR (with contemporaneous effects) to a reduced form VAR results in correlated errors. While OLS remains unbiased and consistent, it is not the most efficient estimator under the presence of correlated errors. Generalized Least Squares (GLS) can be used to efficiently estimate the parameters by accounting for the correlation among the error terms.

Infinite VMA representation

Provided that the VAR is stationary it admits to an infinite vector moving-average (MA) representation.

Let’s consider the reduced form VAR model in Equation (5), we can backward substitute the lagged values to obtain,

If we continue this iteration \(n\) times we get,

If we continue this an infinite number of times we get,

where \(\mu = (\bar{x}, \bar{z})^{'}\), \(\bar{x} = \frac{a_{10}(1-a_{22})+a_{12}a_{20}}{(1-a_{11})(1-a_{22})-a_{12}a_{21}}\), and \(\bar{x} = \frac{a_{20}(1-a_{11})+a_{21}a_{10}}{(1-a_{11})(1-a_{22})-a_{12}a_{21}}\).

Stability and stationarity

In an AR(1) model, \(y_t = a_0 + a_1 y_{t-1} + \epsilon_t\), the condition for stationarity is that \(|a_1|<1\). There is a direct relation to this condition and the stability condition for a VAR model. The VAR model is covariance-stationary if the shocks of \(\epsilon_t\) goes to zero over time. This is the case if the eigenvalues of \(A_1\) are less than one in absolute value.

When looking at the moving average representation in Equation (21), we can think of if the \(A_1\) matrix “blowing up” \(y_t\) such that it goes to infinity, or if it converges back to its mean after a shock.

Generating a VAR series

To generate a time path of a system, i.e., to not estimate the parameters given a dataset but instead generating the data given a set of parameters, we can consider the following Julia code.

using Random
using Plots
using LaTeXStrings

# Set the seed
rng = MersenneTwister(1234);

# Number of observations
n = 100

# Draw normally distributed random numbers
e = randn(rng, 2, 100)

# Define coefficient matrix
A1 = [0.7 0.2;
     0.2 0.7]

# Define vector of constants
A0 = [0 ; 0]

# Pre-allocate the matrix y to store results
y = zeros(size(e))

# Initiate y with x_0 = z_0 = 0, thus only with the innovations
y[:,1] = e[:,1]

# Generate the autoregressive system
for i in 2:n
    y[:,i] = A0 + A1 * y[:,i-1] + e[:,i]
end

# Generate a time vector corresponding to each column in y
time = 1:size(y, 2)

# Plotting y_t
plot(time, y[1, :], label=L"$x_t$", title=L"Plot of $y_t$", xlabel="Time", ylabel="Value",
     legend=:topright, linecolor=:black, linewidth=2)
plot!(time, y[2, :], label=L"z_t", linecolor=:black, linestyle=:dot, linewidth=2)

The code sets the matrix of constants \(A_0\) equal to \([0,0]^{'}\), the coefficient matrix \(A_1\) equal to \(\begin{bmatrix} 0.7 & 0.2 \\ 0.2 & 0.4 \end{bmatrix}\), the initial values of \(x_0\) and \(z_0\) to zero, generates 100 values of \(\epsilon_t\), and from there generates \(y_t\).

The figure below shows generated data for the system.

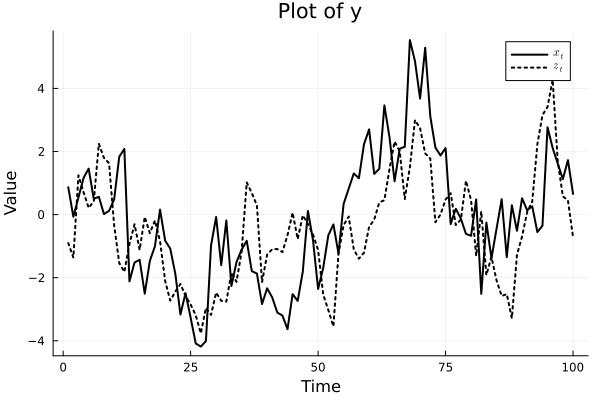
Estimation

The \(A_0\) matrix contains \(n\) parameters and the \(A_1\) matrix contains \(n^2\) parameters, which means that the total number of parameters that need to be estimated is \(n+pn^2\), where \(p\) is the number of lags. Therefore, the number of parameters grows quickly as the number of equations are added to the model and the number of lags increase.

Another consideration is if we can recover the structural parameters from the VAR in Equations (1), (2), (3), and (4), by first estimating the reduced form? Remember that we cannot immediately estimate the structural Equations (1) and (2) since the regressors are correlated with the error term.

The fact is that we cannot recover the structural parameters unless we put some restrictions on our reduced form model. The reason for this is that the OLS estimation of the reduced form model, Equation (5), yields the following parameters \(A_0\) (2 parameters), \(A_1\) (4 parameters), the calculated variance-covariance matrix of the errors (2 variances, and 1 covariance), this sums to 9 parameters, whereas the structural Equations (1) and (2) have 10 parameters (8 coefficients and 2 variances of the two errors). This means that the structural model is “under-identified”.

In order to deal with the under-identified structural VAR system, it is necessary to restrict at least one parameter. This can be done by economic intuition, e.g., if we have an economic reason to set one variable equal to, e.g., zero.

Another, and perhaps the most common approach to deal with the under-identified structural model, is to use the Cholesky decomposition. With this approach we are setting one of the contemporaneous effects of the variables equal to zero. I.e., either \(b_{12}\) or \(b_{21}\) is equal to zero.

Assuming that we use the Cholesky decomposition and set \(b_{21}\) to zero, then we can use the recursive method outlined by Sims (1980) to estimate all parameters. In particular, given \(b_{21}=0\), Equations (11) and (12) become,

Which means that,

Equations (24) through (26) are 3 equations and 3 unknowns, which is solvable. The reduced form estimated variance-covariance matrix consists of \(var(e_1)\), \(var(e_2)\) and \(cov(e_1, e_2)\), after calculating these, we can solve for \(b_{12}\) and lastly for \(\sigma_y^2\).

Impulse response function (IRF)

The reduced form model in Equation (5) can be rewritten into its infinite VMA form in Equation (21). The VMA representation is useful when tracing out how a shock is affecting the system. Let’s write out the infinite VMA representation,

Equation (27) expresses the variables \(x_t\) and \(z_t\) in terms of the reduced form errors \(e_{1t}\) and \(e_{2t}\). However, it is helpful to rewrite this expression in terms of \(\epsilon_{xt}\) and \(\epsilon_{zt}\), the errors in the structural representation. We can solve for \(\epsilon_{xt}\) and \(\epsilon_{zt}\) from Equations (11) and (12),

Therefore, we can rewrite Equation (27) as,

This notation is a bit messy and therefore it is typically written as,

Or on the more compact form,

Where,

The coefficients of \(\Phi_i\) are called impulse response functions and can be used to generate the effects of shocks to \(\epsilon_{xt}\) and \(\epsilon_{zt}\) throughout the entire system. E.g., the coefficient \(\Phi_{12}(0)\) is the instantaneous effect of a one-unit shock in \(\epsilon_{zt}\) on \(y_t\). Similarly, \(\Phi_{12}(1)\) is the one-period effect of \(\epsilon_{zt-1}\) on \(y_t\). Note that the time index can be shifted, and that the coefficient \(\Phi_{12}(1)\) also represents the response of \(\epsilon_{zt}\) on \(y_{t+1}\).

We can calculate the total effect (cumulative response) of \(\epsilon_{zt}(i)\) on \(y_t\) by,

Remember that we need to make further restrictions to the reduced form parameters to fully identify the structural model. Knowledge of the \(A_0\) and \(A_1\) matrices and the variance-covariance matrix is not enough. Again, the most common method to fully identify the structural model is the Cholesky decomposition. Here we assume that \(x_t\) does not have an contemporaneous effect on \(z_t\) as we set \(b_{21}=0\).

One important thing to keep in mind when using the Cholesky decomposition is that we introduced an artificial ordering in the system. An \(\epsilon_{zt}\) shock directly affects \(e_{1t}\) and \(e_{2t}\), but an \(\epsilon_{xt}\) shock does only affect \(e_{1t}\). \(z_t\) is called “causally prior to \(y_t\)”. This implies that depending on how you run your reduced form VAR, i.e., how you order your \(x_t\) and \(z_t\) data, you will have different assumptions in your model. In fact, if you use Stata (a statistics software program), the IRFs are automatically ordered without informing the user, meaning that you will get different results depending on how you structure your dataset.

IRF example

Let’s again consider the following model,

Let’s further assume that the Cholesky decomposition is performed such that \(b_{21}=0\) and that \(b_{12}=0.8\),

This means that a shock in \(\epsilon_{zt}\) has no contemporaneous effect on \(x_t\) and only an contemporaneous effect on \(z_t\). However, \(\epsilon_{xt}\) has contemporaneous effects on both \(z_t\) and \(x_t\).

using Plots
using LaTeXStrings

# Number of observations
n = 20

# Define coefficient matrix
A1 = [0.7 0.2;
     0.2 0.7]

# Define vector of constants
A0 = [0 ; 0]

# Cholesky restriction on B
B_cholesky = [1 0;
              0.8 1]

# Create a unit shock shock to epsilon_xt and keep everything else 0
shock = [0; 1]
#shock = [1; 0]

# Pre-allocate the matrix y to store results
y = zeros(2, n)

# Generate the IRFs with 20 lags
for i in 1:n
    y[:,i] = A0 + A1^(i-1) * B_cholesky * shock
end

# Generate a time vector corresponding to each column in 'y'
time = 1:size(y, 2)

# Plotting
p = plot(time, y[1, :], label=L"$x_t$", title=L"Unit shock to $\epsilon_{zt}$", xlabel="Time", ylabel="Value",
     legend=:topright, linecolor=:black, linewidth=2)
plot!(time, y[2, :], label=L"z_t", linecolor=:black, linestyle=:dot, linewidth=2)

Note that the code is not optimally written, but instead written for demonstrative purposes. E.g., it is inefficient to recalculate the exponent of \(A_1\) in each iteration.

Below are one plot for each shock,

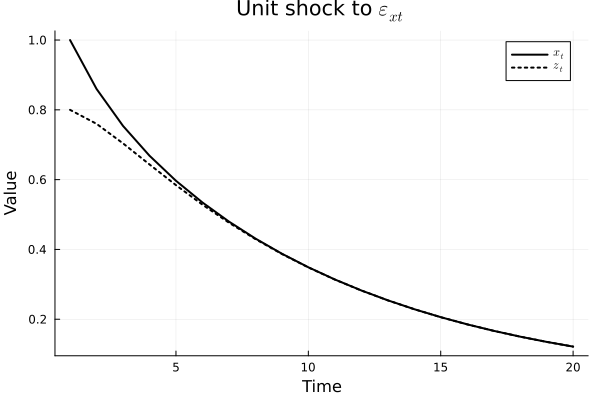
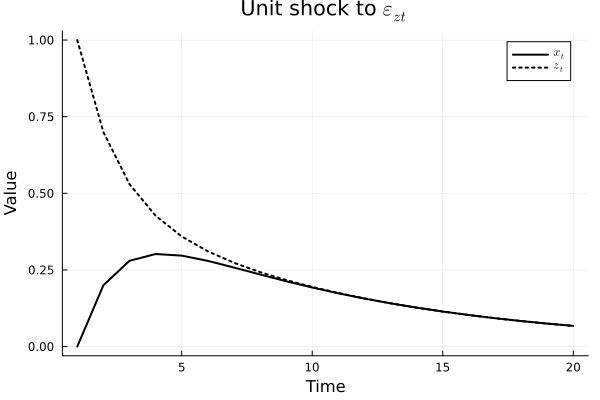
Note that the ordering here is crucial. Since the system is symmetric, if the order were the other way around, we would have the same IRFs but with changed variables.

The ordering becomes very important is the contemporaneous correlation is large, and we need to make a decision on which effect to keep. However, if the correlation is very small, e.g., close to zero, the ordering would not really matter. In this situation, \(\epsilon = e\), since both \(b_{12}\) and \(b_{21}\) are zero. We can test that the correlation is equal to zero if we are unsure. If the correlation is significant and we have no economic reasoning for setting one of the contemporaneous effects to zero, we want to impose the Cholesky decomposition and test both orderings.

Confidence intervals on IRFs

The IRFs are created with the estimated coefficients of the VAR, which means that they are not analytically precise. Therefore, it is common practice to simulate confidence intervals for the IRFs.

As an example, if we think of an AR(1) model specified as \(y_t = 0.6 y_{t-1} + \epsilon_t\), where \(0.6\) has been estimated with a t-statistics of \(4\). In this case, the coefficient is statistically significant and a unit shock to \(\epsilon_t\) will affect \(y_t\) with \(1\) at time \(t\), with \(0.6\) in \(t+1\), and \(0.6^2\) in \(t+2\). The IRF can be written as \(\Phi(i)=0.6^i\). However, the coefficient has a standard deviation of \(0.15 = 0.6/4\), and it is therefore a \(95\%\) chance that, the coefficient is within two standard deviations of \(0.6\), i.e., in the interval \([0.3, 0.9]\). Therefore, the IRF could be anywhere between \(\Phi(i)=0.3^i\) and \(\Phi(i)=0.9^i\).

Now, when dealing with higher-order VAR models it is not as straightforward as to analytically calculate the confidence intervals. The coefficients can be correlated with each other, you may not want to assume normality, and so on. Therefore, it is common practice to perform a Monte Carlo simulation to obtain the confidence intervals:

1. Estimate the VAR coefficients and save the residuals.
2. Draw a random sample based on the saved residuals. Most software packages will draw with replacement a selected sample from the saved residuals, this leads to a bootstrap confidence interval. Since the residuals can be correlated with each other in a multivariate VAR, you can draw the first residual and then pick the other residuals in the same position. This will maintain the proper residual structure.
3. Create a simulated series of \(y_t\) based on the bootstrapped residuals. This is the same practice as when we generated the original \(y_t\) above in section “Generating a VAR series based on the bootstrapped residuals. This is the same practice as when we generated the original \(y_t\) above in section “Generating a VAR series”. Be sure to appropriate initiate the condition, to eliminate any bias.
4. Estimate new coefficients and create new IRFs.
5. Repeat several thousand times, generate several thousands IRFs, and create the confidence intervals. E.g., you exclude the highest \(2.5\%\) and the lowest \(2.5\%\) to create a \(95\%\) CI.

One benefit with the bootstrap methodology is that you do not have to make any distributional assumptions about the residuals.